Diffie Hellman Key Exchange

December 14, 2023 · 3 min read

Developer

This is a cryptographic key exchange algorithm that is used to securely trasmit a shared secret key between two parties over a insecure channel This is not a cipher

The whole purpose of this algorithm is to generate a shared secret key between two parties over a public channel in a secure manner
So people use this method or protocol to generate shared secret between them and then use a symmetric key cipher that uses only one key for encyption and decryption and use this key sending messages in a secure communication channel

Listen, this algorithm is considered as a part of public key cryptography
Why but, as we are generating a secret key, why ???
See, there are some public elements that are shared by both parties which are the same thing - they are public - so here, we have two parameters that is p and g - which are used for individual calculations by both parties and each of them - when they finish their calculation with this public elements, each of them have their public key - which is then shared to one another - then each of them use their private key to find the final shared key

In a nutshell

In the Diffie-Hellman key exchange:

Public Elements (Shared Parameters):

Both parties agree on public parameters p and g, which are shared openly.

Private Keys (Secret):

Each party generates its own private key secretly and does not share it.

Calculation of Public Keys:

Using the agreed-upon p and g and their respective private keys, each party calculates its public key.

Exchange of Public Keys:

Each party shares its public key with the other party over the public channel.

Shared Secret Calculation:

Both parties use their own private key and the received public key to compute a shared secret key. The same shared secret is derived independently by both parties.

This shared secret key, calculated independently by each party but based on the same private and public elements, is then used for subsequent encryption or cryptographic operations.

So in short - diffie hellman key exchange algorithm is used generate and securely trasmit shared secret key between two parties over a insecure channel
So first, we have our public parameters, then using those public parameters p and g, each individual generates their own private key - then they use this private key and the public parameters to generate a public key and send these to each other - then each of them use the received public key with their private keys to generate the shared secret between both parties
So let's break it down how it works -

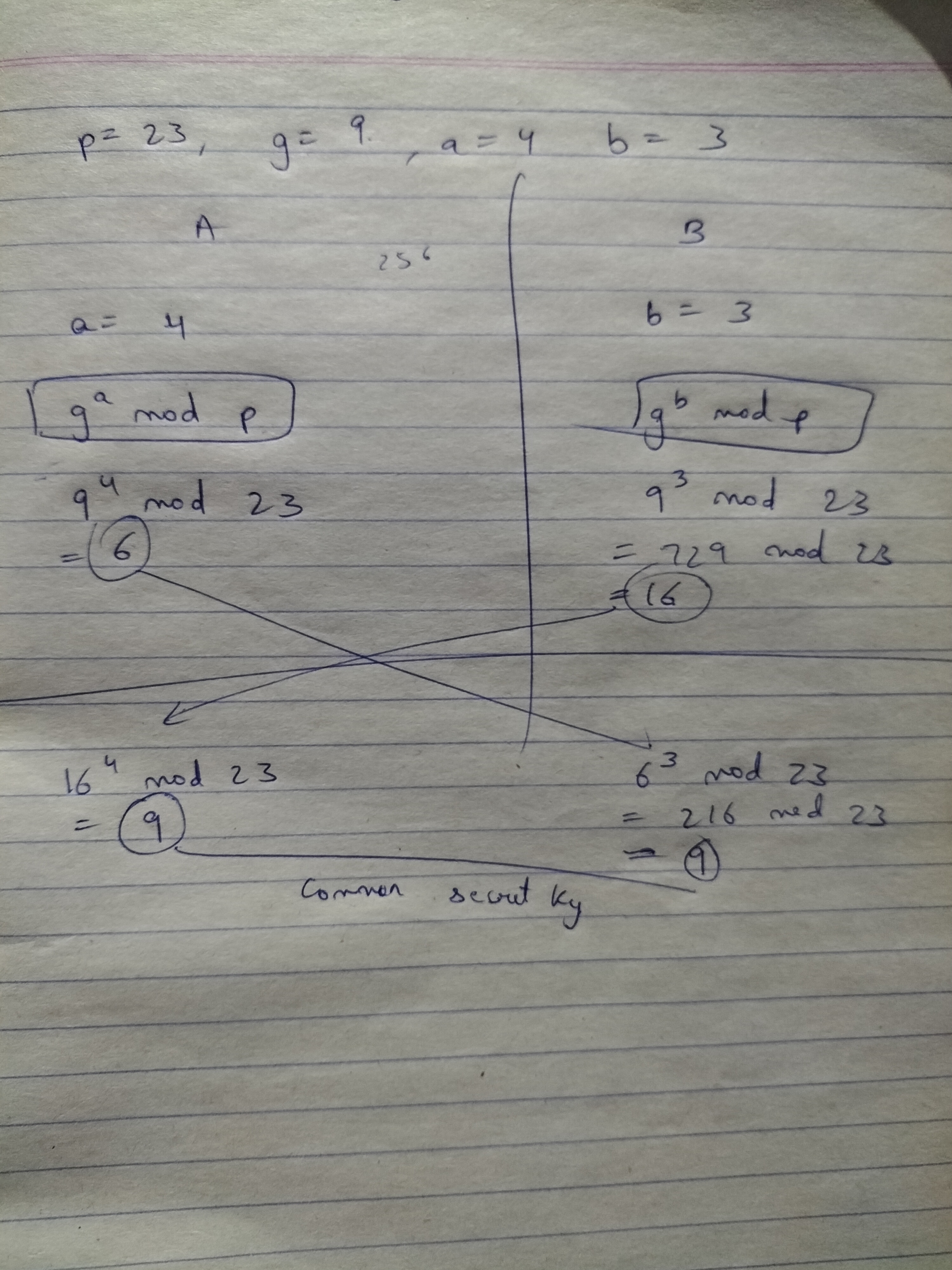
First, assume that A and B already have p and g as they are public parameters
A chooses a random integer a which is less than p - 1. so a is a random integer that is less than p-1 .
Compute g^a mod p - this is going to be called the partial key , i said public eariler but call them as partial keys
Partial keys are generated by the public values and the private random integer that a individual has - this is how they are generated and send to the other party
Send the generated g^a mod p partial key over to the other party B - Now, B party receives this g^a mod p partial key - note that this partial key is going over a insecure channel - anyways, once it goes over to B - then B does the same thing as A
So B is going to first choose a random integer b and then use it to compute g^b mod p - this is the partial key of B - g^b mod p
Now that B has its partial key generated using its private random integer and the public parameters, it sends it over to the other party that is A
So now that A has sent its partial key over to B and vice versa - now there is going to be one operation that is going to be common between both
Both uses the received partial keys to compute - g^ab mod p - so what i mean is - A is going to receive g^b mod p - here we use the exponentiation on this partial key with the private key of A - so it is eventually going to be g^ab mod p - the same thing happens with B. The result of g^b mod p is going to be the shared secret key that both of the parties share - now they can use any symmetric key algorithm with this key to encrypt and decrypt messages