History Of Cryptography
Humans have two basic needs when we take about communication. One is the need to communicate selectively, to communicate and share information. These two basic needs while communicating gave rise to coding and encrypting the messages in such a way that only intended people could have access to the information.
Concepts we should be familiar with
What is a cipher ??
A Cipher is a algorithm for performing encryption and decryption - a series of well defined steps that can be followed as a procedure
What is cryptography ??
Cryptography is the practice and study of techniques for secure communications between two parties
What is Transposition cipher ??
Here the units of the plaintext are rearranged or shuffled without changing the actual letters themselves using a key
What is a substitution cipher ??
In cryptography, a substitution cipher is a method of encrypting in which units of plaintext are replaced with the ciphertext, in a defined manner, with the help of a key; the "units" may be single letters (the most common), pairs of letters, triplets of letters, mixtures of the above, and so forth. The receiver deciphers the text by performing the inverse substitution process to extract the original message.
Table Of Contents
Caeser Cipher
In cryptography, a Caesar cipher, also known as Caesar's cipher, the shift cipher, Caesar's code, or Caesar shift, is one of the simplest and most widely known encryption techniques. It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number of positions down the alphabet. For example, with a left shift of 3, D would be replaced by A, E would become B, and so on. The method is named after Julius Caesar, who used it in his private correspondence. As with all single-alphabet substitution ciphers, the Caesar cipher is easily broken and in modern practice offers essentially no communications security.
Wikipedia - Caesar cipher
In cryptography, a Caesar cipher, also known as Caesar's cipher, the shift cipher, Caesar's code, or Caesar shift, is one of the simplest and most widely known encryption techniques. It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number of positions down the alphabet. For example, with a left shift of 3, D would be replaced by A, E would become B, and so on. The method is named after Julius Caesar, who used it in his private correspondence.
In simple words - this cipher is used to encrypt the plain text by taking each letter of the plain text and shifting them to the right or left (depends on which direction we are deciding to) shift of key , this key is the shift parameter that we provide and this value determines the cipher text that results after encryption
We can also represent encryption in the form of modular arithmetic by transforming each letters into numbers, so A would be 0, B would be 1 and so on. Encryption of a letter x by a shift n can be described mathematically as -
Enigma Cipher -
Enigma Machine - A German Cipher Machine
Enigma machine is a cipher device that was used during mid 20th century by German for dipomatic, commercial and military communication
How does it contribute to encrypting and decrypting messages ??
The Enigma has an electromechanical rotor mechanism that scrambles the 26 letters of the alphabet. Now is this machine used ??? In use, one person enters the text on the enigma's keyboard and another person writes down which of the 26 lights above the keyboard illuminated at each keypress If plain text is entered, the illuminated letters are cipher text Entering ciphertext transforms it back into readable plaintext So at each key press, enigma performs complex substituions resulting in the cipher letter we get from the illuminated light
The main thing to notice that is the security of the system depends on the machine settings - when the nazi were using it to encrypt messgaes, the settings were changed daily. So the receiving station would have to know the same exact machine settings of those of the transmitting station in order to decrypt the messages This setting of rotors, the plugboard connections, all of those acted as the symmetric key between both parties for encryption and decryption
Introduction (high level overview)
Encryption
In the context of cryptography, encryption serves as a mechanism to ensure confidentiality. Since data may be visible on the Internet, sensitive information such as passwords and personal communication may be exposed to potential interceptors.The process of encrypting and decrypting messages involves keys. The two main types of keys in cryptographic systems are symmetric-key and public-key (also known as asymmetric-key) Many complex cryptographic algorithms often use simple modular arithmetic in their implementations
Symmetric Key Algorithms
As we know that there are two types of keys in cryptography - symmetric and asymmetric
what is symmetric key
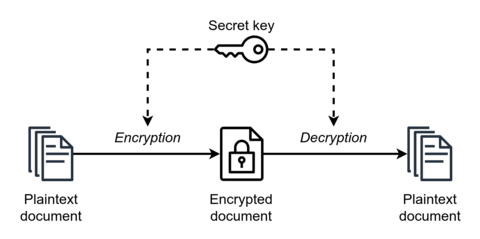Symmetric key cryptographic algorithms use only one single key for encryption and decryption - what this means is, when the plain text is encrypted, a cryptographic symmetric key is used - and when the cipher text is decrypted, the same key that was used in encryption is going to be used for decryption of the cipher text
Easy hai - And we should know that in such algorithms that use symmetric key, the necessary requirement is that the communicating parties should have access to the shared secret key - Due to this, asymmetric key encryption is often used to exchange the secret key for symmetric key encryption
Now you might ask - Brother, we understand what is symmetric keys and they are used in algorithms for encryption and decryption, but can they be used in any kind of ciphers ??
No, symmetric key encryption can use either stream cipher or block cipher
This is interesting
Stream ciphers encrypt the digits (typically bytes), or letters (in substitution ciphers) of a message one at a time.
Block ciphers take a number of bits and encrypt them in a single unit, padding the plaintext to achieve a multiple of the block size. The Advanced Encryption Standard (AES) algorithm, approved by NIST in December 2001, uses 128-bit blocks.
Asymmetric i.e Public key Cryptography
In this cryptographic system, a pair of related keys are used Each pair consists of a public key and private key In asymmetric key encryption scheme, anyone can encrypt messages using the public key, but only the one who is holding the other key of the paired keys i.e private key can decrypt such message….. Here the security of the system depends on the secrey of the private key - which must not become known to any other
You might ask this -
Taha, you said that only two types of keys are there which can be used in cryptographic systems, the systems where we use one key is symmetric key cryptography and the cipher algorithms that are used can be either stream cipher or block cipher For both of these ciphers, we require only one cipher key which can be easily managed But the thing is - In public key cryptographic systems, we can use ciphers - but for those ciphers, two keys are required And its not that we can take any two keys at random - we need two keys that are related to each other So for generating such keys, we have some algorithms - not ciphers - We have Algorithms
In a public-key encryption system, anyone with a public key can encrypt a message, yielding a ciphertext, but only those who know the corresponding private key can decrypt the ciphertext to obtain the original message. For example, a journalist can publish the public key of an encryption key pair on a web site so that sources can send secret messages to the news organization in ciphertext. Only the journalist who knows the corresponding private key can decrypt the ciphertexts to obtain the sources' messages—an eavesdropper reading email on its way to the journalist cannot decrypt the ciphertexts. However, public-key encryption does not conceal metadata like what computer a source used to send a message, when they sent it, or how long it is. Public-key encryption on its own also does not tell the recipient anything about who sent a message—it just conceals the content of a message in a ciphertext that can only be decrypted with the private key.
Hashing
In cryptography, hashing is a process that involves converting an input (this input can be a message or some data) into a fixed-size string of characters…. this fixed size string is what we call hash value or hash
Hashing is commonly used -
- To verify the integrity of data
- Creating digital signatures (i'll explain about these later)
- Store passwords
Working
Input data -
First, you take some data or message which is usually referred as messages
Hash function
A hash function is applied to the input data. This function takes the input data and performs various mathematical calculations and operations on it and produce a unique hash value. Hash functions are so coool (don't write coool in your exam paper 🥲) that even a small change in the input is going to drastically impact the final result from the hash function.
Fixed output Length
The cool thing about this hashing process is that - no matter what size or length your input data is - the hash function always produces a output with fixed length
Irreversibiltiy
Always remember - Hashing is a one way process, which means that when you provide a input to the hash function and we get the hash value, it is computationally impossible to reconstruct the original input data…. this is used to ensure integrity of data in cyber security
Deterministic
If you take some input and provide to the hash function and then you get the hash value, the same hash value is going to be generated no matter how many times you do it…. hash function always produces same hash value for the same input - makes sense to be honest
Collision Resistance
A good hash function should make it really difficult to find two different input that provides the same hash value, this property is kown as collision resistance
My personal experience
Once i was working on a project where the passwords were hashed and salted, and then the passwords were stored in the database, hashed passwords that is So that when the user logged in, we do not take the hashed password from the db and then reverse it back to the way it was originally, what we do is - take the user input, hash it and then compare it with the one that was stored in the DB, if those two match then its all good This way, the password is only known to the users
Digital Signature
A digital signature is a cryptographic technique used to ensure the authenticity, integrity, and non-repudiation of electronic documents, messages or data. It provides a way to verify that the content of the digital item (it can be a document or a message or something that is a digital entity) has not been altered since it was signed and that the signature itself is a valid signature (meaning, that the signature is coming from the right source)
Analogy -
You have a document that you send to your friend, how is he going to know that it is sent by you and how is he going to know that the document that you sent in the initial stage (the original document) - is the document that your friend received ?? how are we going to know these two answers above ?? Here we can use digital signature
Working
Signing process -
The signer generates a pair of cryptographic keys We did study that when we talk about two keys or pair of keys, the one that comes to mind is asymmetric keys - which are public and private keys So the signer generates two keys - public and private key The private key is used by the signer and kept secret - it is used to create digital signatures The public key is widely shared and this public key is only used by others to verify the signature So what we learn from this is -
- Private key to create signature
- Public key to verify signature
This is the overall signing process of a digital signature
Creating the signature
How does the signer create a signature using only the private key ?? To sign a document, the signer uses a hash function to generate a hash value (digest) of the document content. The hash value is then encrypted using the private key. This encrypted hash value is the digital signature.
Verification process
To verify a signature, the recipient of the document uses the signers public key to decrypt the encrypted hash value i.e the digital signature - revealing the original hash value of the document contents
Note -
The recipient receives the document as well as the signature, so dont be confused when i say that the document is hashed - you might ask which document, so know that the document is also present in this verification process
The recipient then generates a new hash value of the document's content (the documents that the recipient received) using the same hash function If the decrypted hash value matches this new hash value that is generated using hash function, this ensures that -
- The document was not altered since it was signed
- Non-repudiation - signer cannot deny that he has signed the document
- Authenticity - it is likely that it was signed by the right owner
MAC (Message Authentication Code)
A message authentication code (MAC) is a cryptographic checksum or tag that is generated and appended to a message to ensure it's integrity (ensuring the message is not changed) and authenticity (the person who has sent it is the valid sender). A MAC provides a way to verify that a message has not been altered during transmission and it was sent by the expected sender. It is created using a secret key and a specific algorithms along with the message
simple words mei -
You take the message, use a secret key i.e symmetric key to create a MAC code which is attached to a message and then they are sent to the receiver The receiver can verify that the message is not altered when it was being transmitted and it was sent by the expected sender by using MAC
Algebra -
Groups and Abelian Groups
Groups
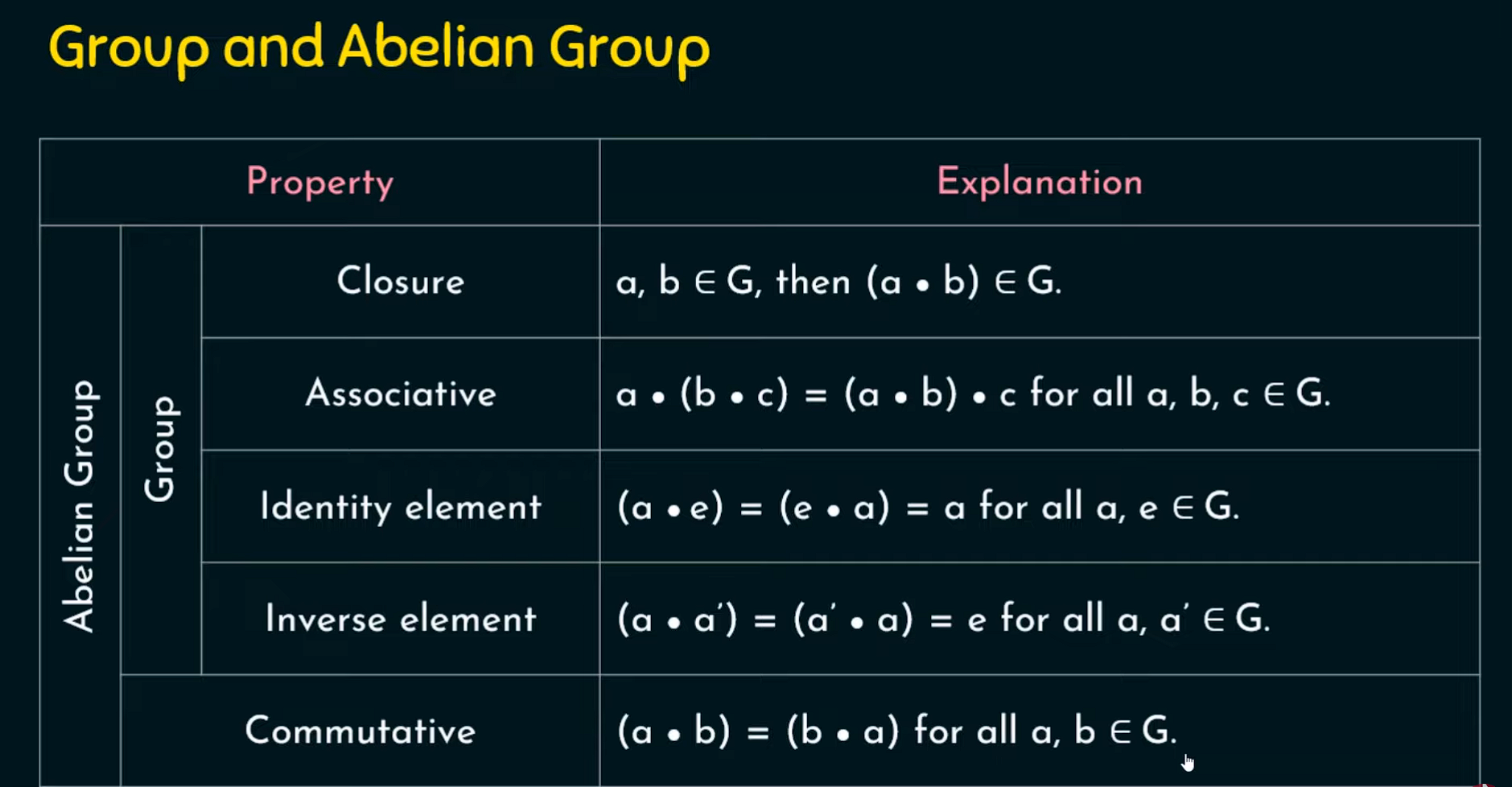
A group G denoted by {G, •} is a set under some operations (•) if it satifies the CAIN properties
What is a group in simple terms ?
A set, where the set of elements under some operation satify some properties is called a Group
A group is a set, where the elements in this set - under some operation satify some properties
What are these properties
CAIN
C- ClosureA- AssociativeI- IdentityN- inverse
Abelian Group
A group is said to be Abelian group if it is already a group and a additional property is also satisfied by the set of elements, and that is Commutative property i.e (a • b) = (b•a) for all a,b in G
What does this mean though ??
see, i told you that a group is said to be a group only when the elements in it satisfy some properties under a single operation. So in order to satify each propertym we have some things we need to prove as we can see above
Note -
We can take any elements from the group for each property to be satisfied, so it is not that we have to take two elements in the beginning and use that for every single property.
Notations -
We have few notations in number theory for sets
- N → Set of all natural numbers
- W → Set of all whole numbers
- Z → Set of all integers
- C → Set of all complex numbers
- Q → Set of all rational numbers
- R → Set of all real numbers
Z+- set of all positive integers onlyZ-- set of all negative integers only
Rings, fields
What is a ring ??
A ring R denoted by {R, \*, +} is a set of elements with two binary operations, called addition and multiplication such that for all a,b,c ∈ R
the following axioms are obeyed
- The set should be a abelian group
(A1 - A5)(first it should be a group) : + related. here A means addition, so the set should be a abelian group under + - Closure under multiplication
(M1): So any two elements from this set, if a,b ∈ R thenab ∈ G - Associativity of multiplication
(M2): a (bc) = (ab) c ….. for all a,b,c ∈ R Here, the result should be equal on both the sides, and all the elements a,b and c should belong to G - Distributive laws
(M3)-
Here we use both the symbols + and *, not just one like we do for associative for addition and associative for multiplication
So we have two laws
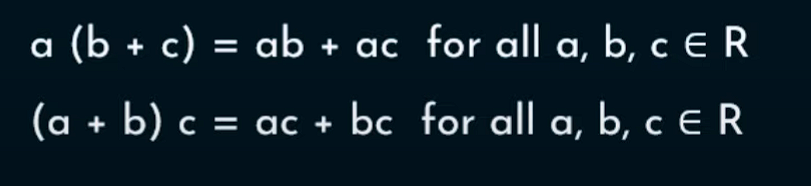
See - it is easy A set of elements is said to be a ring - when it is a -
- A abelian group
- Closure under multiplication is satisfied - M1
- Associativity under multiplication is satisfied - M2
- Distributive laws must be satisfied as well - M3
All these conditions - when they are satisfied for a set, that set is said to be a Ring
What is a commutative ring ??
A ring is said to be a commutative ring, if it satisfies the following additional conditions
Commutativity of multiplication (M4) : ab = ba for all a,b ∈ R
What does this mean ??
A set - when it satisfies the properties A1, - A5 under addition - which is, the set should be a abelian group - anddd now the abelian group or the set we have also satisfies - M1, M2, M3, which makes the group a ring
Now that the set is a ring - if it satisfies another additional condition which is M4 as we have seen anove, the ring is said to be a commutative ring
What is Integral Domain ??
A integral domain is a commutative ring (A1-A5 and M1-M5 are satisfied) that obeys the following axioms -
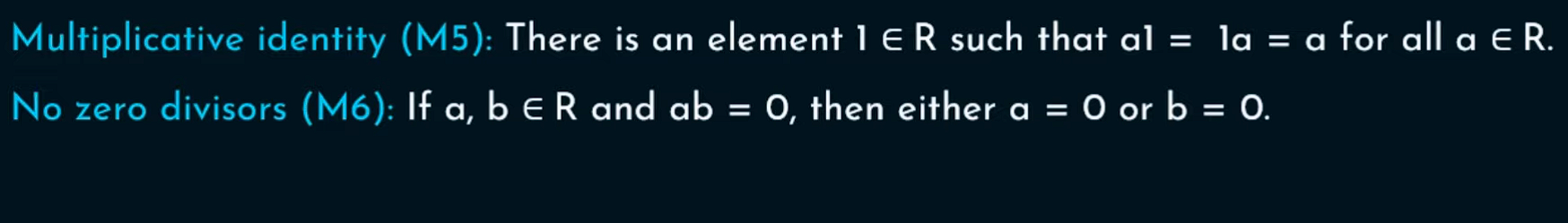
M5 here is a condition that says that there is an element 1 that belongs to R, so the element is 1 that belongs to R such that a*1 = 1a = a *for all a belonging to R
What M6 axiom says is - if you take any elements a and b from the commutative ring and ab = 0 then either a = 0 or b = 0
Just know about this that -
Integral domain - A1 to A5, M1 to M6
What is a Field ??
So a field is a integral domain that satisfies one more axiom and that is - for each a in the F except 0, there is an element that is inverse of it in F such that -
a * a inverse = 1
OR
a inverse * a = 1
Any one of this condition, equals to 1 - then the condition is satisfied
Summary
Very important thing to note
Identity element can depend on the operation
What do i mean ??
In number theory, an identity element refers to a specific element within a
mathematical operation that leaves other elements unchanged when combined
with them under that operation
So for addition, identity element is 0
as you add any element and it will be unchanged
In multiplication,
the identity element is 1 because any number multiplied by 1 remains the
same
One more thing -
You might think, what is this multiplicative inverse and multiplicative identity
They are just Identity element under multiplication and Inverse element under multiplication operation……
One last note -
- The result of a inverse element condition under addition needs to be the identity element of that operation
- So if we are satisfying the inverse element condition under addition then the result of LHS and RHS should be 0
- Same goes for multiplication, the result should be 1
RSA
Rivest Shamir Adleman - RSA is a asymmetric key algorithm.
here two keys are used, public and private where messages are encrypted using public key and the only way to decrypt the messages is using the private key
Note -
plain text and cipher text are integers between 0 to n-1 for some value n
What is a modulus ??
In our case, we can consider modulus to be a number where when we use it to perform modular operation, then the result is going to be "wrapped" in the range of 0 to modulus - 1
What is euler's totient function
- This function counts the number of positive integers that are less than or equal to n that are relatively prime to n
- By relatively prime, i mean they are co-prime to n
- So all numbers that are less than n that are not multiples of p and q will be coprime to n
- So that we why we say - ∮ n = (p- 1) * (q - 1)
RSA has three phases
Three Phases -
Key Generation
First off, we generate the keys we need for encryption and decryption
Remember that this algorithm is a cipher - we are securing a message by encrypting and decrypting it - we are not just done by finding two keys and then boom - No, we also need to perform cipher operations
- Select 2 large prime numbers p and q - higher the values, higher the level of security in the keys
- Calculate the modulus n = p*q
- Find the count of all positive integers that are coprime to n
We do that by using eulers totient function
Phi of n = (p - 1)*(q - 1) - Choose e such that
- e should be greater than 1 and less than phi of n
- e should be co prime to n i.e gcd(phi of n, e) should be equal to 1
- Choose d
ed mod phi(n) = 1
Note
- Note that when calculating e and d, we are using the phi of n of n and not the n itself, leading to the fact that e is within the range of phi of n and a coprime to n as well as d * e is a number that one digit bigger than the phi of n
- So the magic in d is that by multiplying it to e, that product of e and d, it should be a number that is one digit above the phi of n
-
Public Key -
PU ={e,n} -
Private Key -
PR ={d,n}
Encryption
C = M^e mod n
Decryption
M = C^d mod n
Trick to find d easily
- Now this is my personal opinion, you can solve it however you want
- See, first off we know that e and d both of them are less than φ(n) and e is going to be a co prime to φ(n) - now i think that while selecting e, we should also think about d as well
- First off, in order to find e, what you should do is - first find all of the numbers less than φ(n) that have factors other than 1 to it, we can simply find that -
- If not, then keep on multiplying numbers sequentially and for each result, check with the mod whether the answer is 1
- So make a list of all the numbers that are factors of φ(n) - now that we have them, make another list of all those numbers that are less than φ(n) but they are not in the factors list - this way we have a list of all the numbers that are coprime to φ(n)
- So for now, we have a list of numbers that are coprime to φ(n)
- Now you can select any of the number from this list but very small numbers might not work sometime - so try with some of the numbers
- Now that you have a number selected, this is going to be our
e - How do we find the d now ??
- We use the formula
de mod φ(n)and the result should be 1 - For those who don't know what i am about to say. dont worry - See. d is a multiplicative inverse of e mod φ(n), meaning - d is going to be such a number that when multiplied by e and then - mod φ(n), we get result as 1 as 1 is the identity element for multiplication operation
- So basically d should be such a number that when e is multiplied to it and then that result is mod to φ(n) then the final result is 1
- So what i did is - i created multiplication tables of φ(n) from 1 to 10
- So if we have 60 then 60*1 = 60 and so on till 10
- Why did i do this ??
- See, we are going to start with e, and then multiply natural numbers sequentially to e at a point that we get a number that matches any one of the numbers from the tables of φ(n)
- In simple words - we are going to start from 1,2,3 and so on and multiply them to e and then that result, we check that if it is 1 number greater than any of the tables result of φ(n)
- I know this is confusing
- Let's take a example - consider that in the table of φ(n), we find a mathc for 60*4 = 240. lets say that we find a number d that when we multiply to e - we get 241…. so we keep on multiplying numbers from 1,2 and so on to e so that we find a number like 241 which is one number bigger than 240
- The point of my example is that - we keep on multiplying to e to find d - such that the result of both should be 1 number bigger than any of the tables results, by tables result i mean - for example if φ(n) is 60, then 60, 120, 180, 240 and so on
- This way, first write down e, then keep on mutlipying numbers from 1 to….. just dont stop for a few trials, see that the result is one number greater than any of the numbers in the tables of φ(n)
- Let me give you my experience of how i thought this might be a good way to find d, there might be better ways but i dont have time to find those ways and implement them as exams are coming up in a week
- So what i did was, my φ(n) was 60, so i choose 7 as e, then i kept on multiplying numbers to 7 from 1 and then i found 7*43 - which has result one number greater than one of the tables results and that is 301 which is one number bigger than 300
- That is how i found 43 as my d value
So we have a list of numbers that are co prime to phi of n - those are e and we are also finding d at the same time just to be sure - so what i think would be easier to find d is -
As d is the mutliplicative inverse of e mod n, meaning a number which multiplied to e and then mod n is going to give 1
So first write down the tables of phi of n, which is 60, till 10
Then take the first number from the list of numbers we have for e - then find a mutliple that is going to be a one number bigger than any of the 60 tables we have
Diffie Hellman Key Exchange
Number theory
Prime numbers
A natural number greater than 1 that cannot be exactly divided by any whole number other than itself and 1.
Modular Arithmetic
GCD
GCD stands for greatest common divisor, it is the greatest common factor between two integers, so two integers having many factors, among all of them, the highest and the common factor is known as GCD, if the greatest common factor between two numbers is 1, then both are coprime to one another
Euclidean Algorithm
Euclidiean algorithm proceeds with a series of steps where the output of one step is used as the input to another.
The Euclidean Algorithm (article) | Khan Academy
So this is a quick way of finding GCD between two numbers
How to find GCD using Euclid's algorithm ??
-
If we divide
bbycexplicitly with quotientqand remainedrthenb=c*q+r -
In each subsequent steps, a similar equation is written
-
The new dividend and new divisor are the divisor and remainder from previous step.
-
Continue this process of division and creating similar equations based on previous step's output as input, until the remainder is 0
What does this mean ??
First off, divide b by c so and take the decimal part from the quotient, and the remainder - use this to create a equation such as : b = c * q + r
Now once you have this equation and you put the values as well, repeat this process of creating equations with the same formula but the values are going to be different -
for each next step, the b is going to be previous step's c and the c is going to be previous step's r - and then using b and c, we can have the q and r for our next step - so continue this process of creating equations, until we reach a step where the remainder is 0
So the last step where the remainder is 0, the c in that equation is going to be the GCD.
Euliers Totient function
This function outputs a integer which is the count of positive numbers that are coprime to n, within the range of 1 to n-1
So all the positive integers that start from 1 to less than n - those numbers that are relatively prime to n, the total number of such values is going to be the output for euliers totient function
Here. it is explained very well -
Wikiwand - Euler's totient function